Teoria dos Grafos

Origem

O problema das Sete Pontes

Podemos dizer que a origem da área de estudos dos grafos foi o problema conhecido como Sete pontes de Königsberg

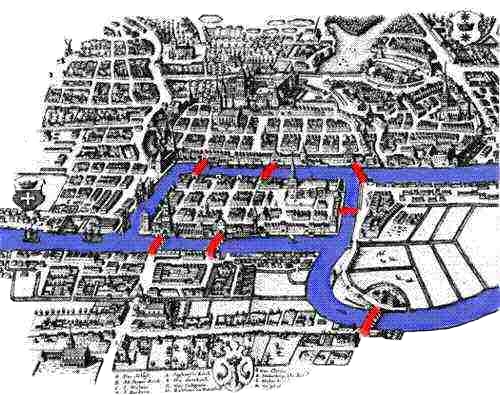
A proposta do problema era simples;

“É possível fazer um passeio pela cidade atravessando cada uma das sete pontes exatamente uma vez, sem repetir nenhuma?”

O debate durou até 1736 quando Leonard Euler conseguiu provar que era impossível, para isso ele usou uma linha de raciocínio bem simples; para existir um caminho que passe por cada ponto exatamente uma vez (chamado caminho euleriano), o grafo deve ter 0 ou 2 vértices de grau ímpar.

se pensarmos um pouco até que faz sentido, se considerarmos um grafo com 3 vértices interligados entre si, é óbvio que podemos iniciar em qualquer ponto e circular por todo o grafo e voltar ao mesmo ponto, e se pensarmos um pouco podemos analisar que esse grafo seria considerado um grafo que segue os princípios da regra acima, já que não teria nenhum vértice de grau impar.

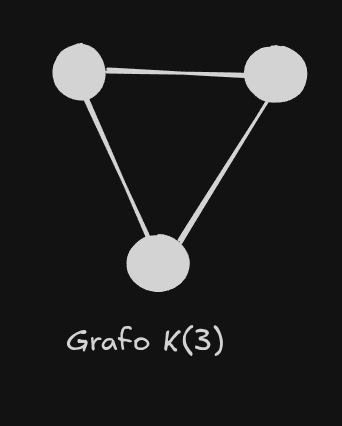
para perceber isso vamos primeiro definir o que é o Grau de um vértice, de maneira bastante simplificada, podemos dizer que o Grau de um vértice é o número de Arestas que estão ligadas nele. isso é bem fácil de se notar, a única característica especial que devemos ficar de olho é em relação a um vértice que tenha uma aresta que liga-se a esse mesmo vértice, chamamos isso de laço

lembrando que estamos aqui tratando de grafos não direcionados, e no caso do exemplo do problema das sete pontes, nada de laços.

voltando ao problema, vamos tentar observar outro grafo que entraria prova de Euler.

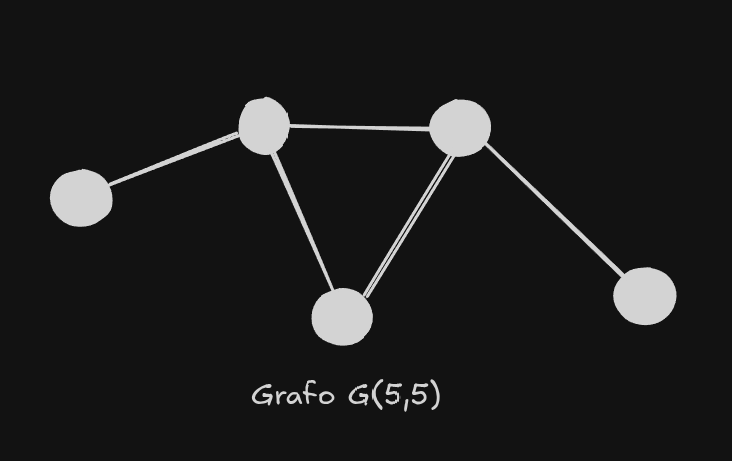
vamos considerar esse grafo G(5,5), ou seja, um grafo com 5 vértices e 5 arestas, olhando assim ficaria meio confuso analisar só lendo meu texto, então vamos adicionar algo para diferenciar as cabeças de gado.

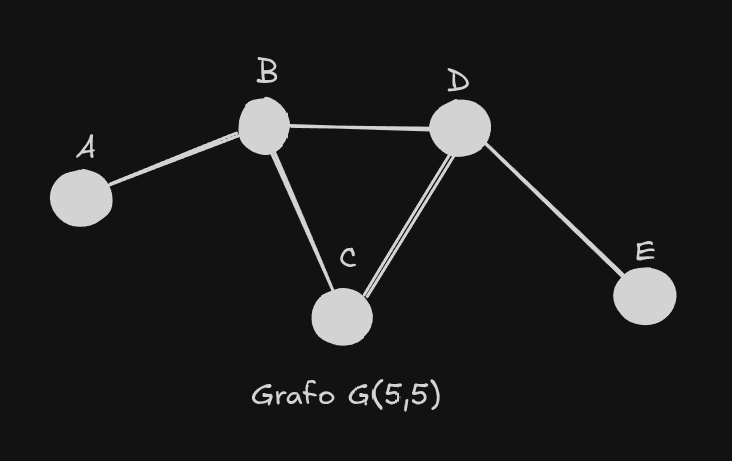
agora com os vértices com nomes apropriados podemos analisar o trajeto de melhor maneira.

vamos aplicar a mesma pergunta do problema das sete pontes nesse exemplo.

“É possível fazer um passeio pelo grafo atravessando cada uma das cinco vértices exatamente uma vez, sem repetir nenhuma?”

olhando para esse grafo podemos perceber que sim é possível, afinal, poderíamos seguir a seguinte sequencia $A\to B\to C\to D\to E$ e no final disso teríamos atravessado todo o grafo sem repetir essa ponte nenhuma vez. Isso por que esse grafo também segue a regra do grafo Eureliano.

Ok, tudo parece fazer sentido até agora, poderíamos até dizer que está fácil de uma maneira ridícula, mas vamos agora testar se essa propriedade realmente se aplica ao adicionar só mais um vértice de grau impar ao grafo.

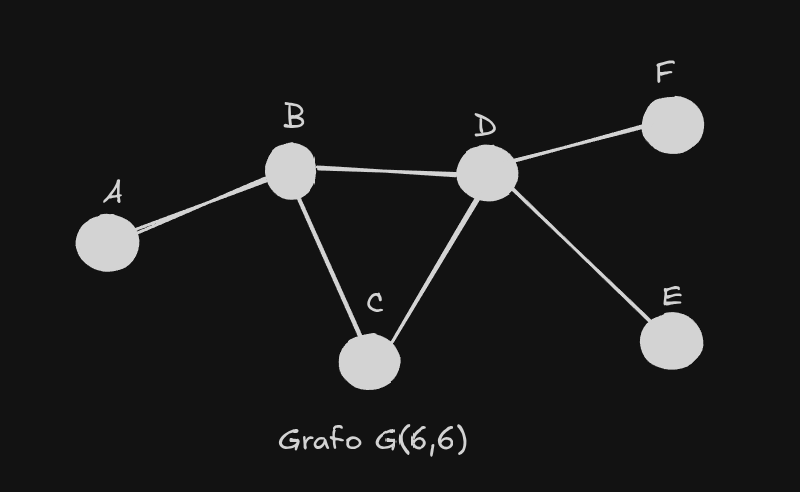
agora vamos tentar seguir a mesma sequencia do anterior $A\to B\to C\to D$

no momento em que chegamos no vértice D temos que fazer uma escolha, mas observe que curioso, independente da escolha que tomar-mos, estaremos automaticamente excluindo a possibilidade de de escolher o outro vértice, se escolher-mos o $E$ estaremos deixando impossível escolher o $F$ já que para chegar nele teríamos que passar novamente pelo $D$, o que quebraria a regra do problema.

tire um tempo para analisar quaisquer outras configurações que sigam esses padrões, pode desenhar no editor de fotos de sua preferencia ou usar o excalidraw para fazer os rabiscos.

O ponto principal por trás dessa lógica está em pensarmos nas situações em que é possível andar por todo o grafo, ou seja, no caso de haver dois ou nenhum vértices de grau impar.

A parte de possuir nenhum é já auto-intuitiva dada o exemplo básico do $K(3)$ mostrado anteriormente, mas o segredo de porque podemos aceitar dois de grau impar é imaginarmos eles como duas portas, uma de entrada e outra de saída, se tivermos 3 portas, no “melhor” dos casos você pode entrar por uma e pode escolher uma das duas para sair, necessariamente você estará excluindo porta que não escolheu.

e nisso voltamos a lógica de Euler:

Para existir um caminho euleriano, o grafo deve ter exatamente 0 ou 2 vértices de grau ímpar.

perceba que com essa simples sentença podemos definir se em um grafo qualquer existe ou não um caminho Eureliano

também existem variações desse problema em que poderiamos repetir uma aresta, no caso seria a aresta de inicio, essa variação podemos denominar circuito, mas abordaremos mais sobre isso posteriormente junto com a diferença do caminho.

O Problema do caminho hamiltoniano

Outro ponto fundamental na origem do estudo dos grafos foi o Problema do caminho hamiltoniano esse por sua vez debatido tanto no na teoria da complexidade computacional quanto na teoria dos grafos.

O problema do caminho hamiltoniano segue uma lógica parecida com o problema das sete pontes, a diferença aqui é que estamos mais interessados nos caminhos que vamos fazer do que nos pontos que vamos passar.

Se pararmos para pensar um pouco obrigatoriamente andaremos por todos os pontos pelo menos uma vez para andar por todos os caminhos, mas o objetivo prático é bastante diferente.

um dos melhores e mais importantes exemplos de problema que podemos citar que tem envolvimento com essa área é o problema do caixeiro viajante. Mas outros muito mais comuns e corriqueiros podem ser citados como por exemplo a construção do desenho de uma placa de circuito impresso, em que se quer gastar a menor quantidade possível de material para chegar nos pontos de solda. Também podemos citar aplicativos de entrega, seja Ifood ou correios, para economizar o máximo de dinheiro deve-se evitar ao máximo repetir uma mesma rua, afinal, se você repetiu uma mesma rua isso significa que provavelmente você poderia ter passado apenas uma vez por essa, gastando assim menos combustivel.

Notação básica

depois de termos debatido um pouco sobre a área, se você é totalmente iniciante talvez acabou por se perder nos termos como Vértices e Arestas.

para solucionar isso, vamos deixar todos os leitores na mesma página com essa pequena tabela

termo	termo matemático	explicação
Vértice	geralmente representado pela letra $V$	podemos entender Vértices como pontos, ou Nós se for mais confortável, eles podem ou não estar ligados a outros Vértices
Arestas	geralmente representado pela letra $E$ de Edge em inglês	arestas, ou Arcos por exclusão são obviamente as retas(ou tortas, nunca se sabe) que ligam dois vértices

Ok, agora sabendo disso podemos trabalhar em algumas representações matemáticas mais avançadas, como por exemplo a definição de um grafo, como podemos matematicamente representar um grafo qualquer?

a maneira mais simples é com a seguinte notação:

$$G=(V,E)$$

ou seja, o Grafo G é uma junção de Vértices e Arestas. para ser mais específico, uma coleção desses mesmos, ou seja:

podemos definir $V$ como

$$V=\{1,2,3,\dots ,n\}$$

já que podemos ter $n$ vértices